- Phase-field modeling of brittle fracture with multi-level hp-FEM and the finite cell method. Computational Mechanics 63 (63), 2019, 1-18 more… BibTeX Full text ( DOI )
Fracture Mechanics
Motivation
Numerical simulation of crack propagation is of major engineering importance and a challenging problem. The main difficulty stems from the inherently discontinuous nature of the crack imposing difficulties to numerical treatment. As an alternative, the phase-field approach to fracture emerged which altogether avoids the modeling of discontinuities by approximating the crack using a diffusive field. The regularization of the sharp crack is based on a length-scale parameter which governs the extent of diffusion and determines the numerical width of the crack. For small length-scale parameters, a very fine mesh is needed at least in the vicinity of the crack to fully resolve the resulting crack profile.
To overcome this challenge, the numerical framework developed at the chair combines multi-level hp-refinement [2] with a phase-field model for brittle fracture to allow for a locally refined mesh which dynamically adapts to the crack path. In a second step, the Finite Cell Method (FCM) [1] was successfully integrated into the model to enable the efficient simulation of complex geometries.
Projects
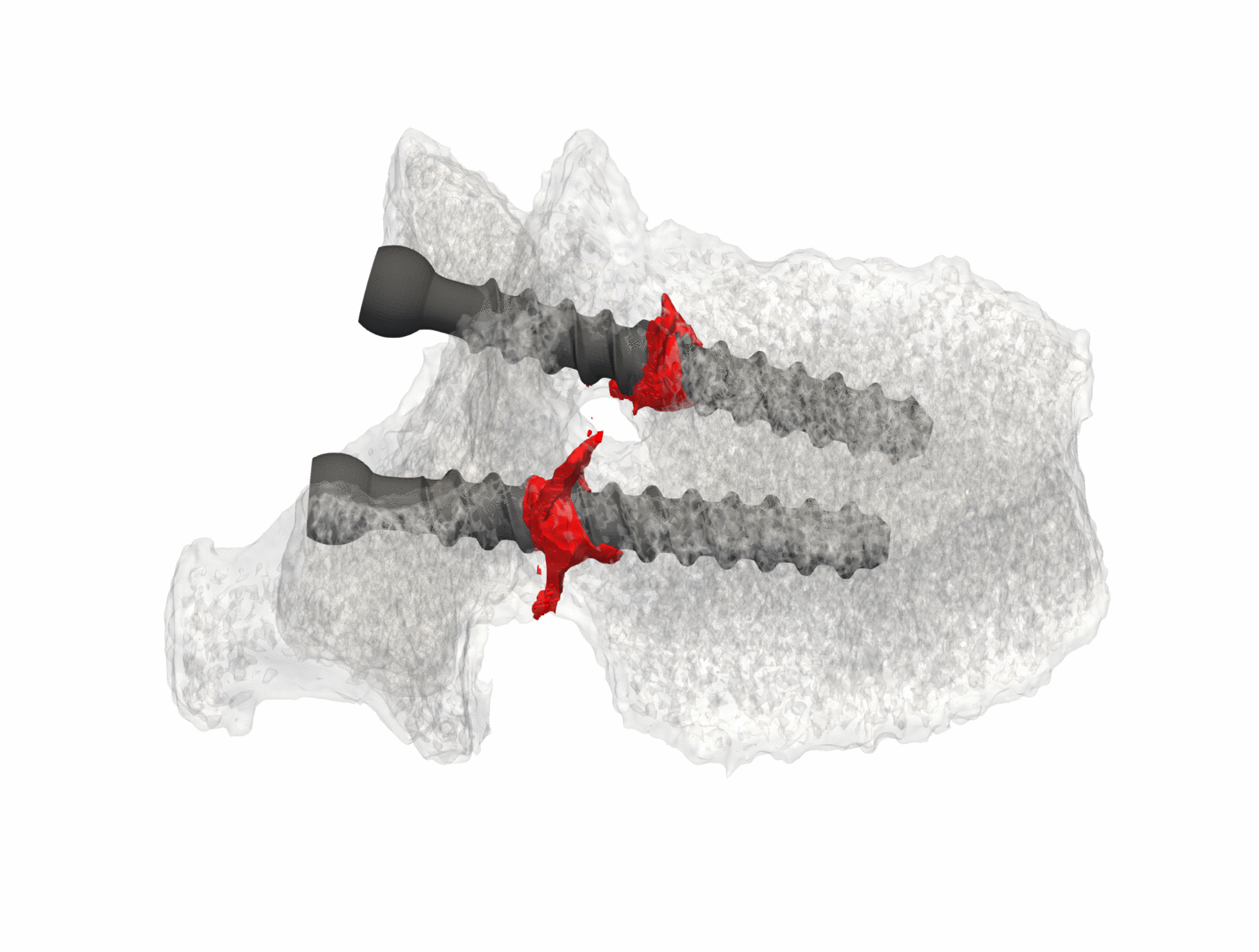
Fracture Risk in Human Bones
Femoral and humerus fractures are common in the elderly population due to osteoporosis, and are often initiated by falling on the side or on an out-stretched arm. Quantifed computed tomography (QCT), combined with empirical data obtained by biomechanical experiments and computational mechanics may provide the means to enhance our understanding of this frequent injury. The central goal of this interdisciplinary project is the prediction of fracture risk by considering the interplay between micro-mechanical and macroscopic bone models, validated by experiments.
| Project team leader | Dr.-Ing. Stefan Kollmannsberger (TUM), |
| Doctoral Researchers | Lisa Hug (TUM), Nina Korshunova (TUM) |
| Principal Investigators | Prof. Dr. rer.nat. Ernst Rank (TUM), Professor Zohar Yosibash (Tel-Aviv University) |
| Funding | International Graduate School of Science and Engineering (IGSSE) |
References
[1] Düster, A., Parvizian, J., Yang, Z., and Rank, E. (2008). The finite cell method for three-dimensional problems of solid mechanics. Computer methods in applied mechanics and engineering, 197(45-48):3768–3782.
[2] Zander, N., Bog, T., Kollmannsberger, S., Schillinger, D., and Rank, E. (2015). Multi-level hp-adaptivity: high-order mesh adaptivity without the difficulties of constraining hanging nodes. Computational Mechanics, 55(3):499–517.