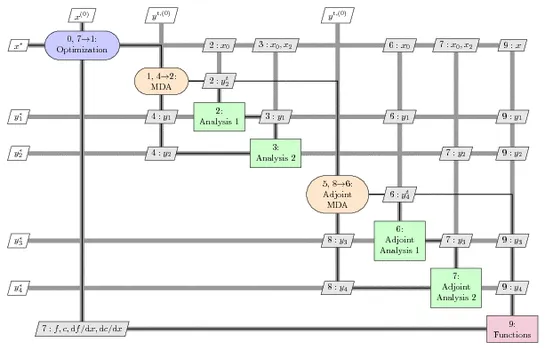
Multi-disciplinary design optimization(MDO) is about finding optimal designs for systems which are controlled by a number of disciplines or subsystems. Although numerical optimization has been successfully applied to computational fluid dynamics(CFD) and computational structural mechanics(CSM) problems, for some applications physically meaningful optimum design can only be identified if the interaction between involved physics is considered. For example, one of the most important applications of MDO is in the field of aerospace engineering in which disciplines like aerodynamics, structural analysis, propulsion, control theory, and economics are involved.
Shape optimization of flexible body in laminar flow
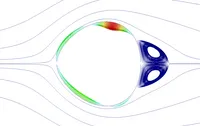
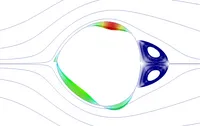
The first application of our optimization framework including the fluid-structure interaction analysis, the coupled adjoint sensitivity analysis and the actual optimization process with the farfield force objective function and the Vertex-Morphing method is presented here. To this end we use a model in which a non-linear cylinder shell is immersed in a laminar incompressible fluid flow.
To see the differences between sensitivity information obtained by single-disciplinary sensitivity analysis (only gradient information from the fluid) and coupled sensitivity analysis, we performed an FSI simulation to obtain the deflected shape of the cylinder and calculate the sensitivities once using our coupled adjoint solver and once using the adjoint fluid solver only, right figures.
Furthermore, the shape evolution for 130 optimization iterations together with the improvement of the combined lift and drag objective function is shown. The latter presents each the undeformed shape according to the updates of the optimizer as well as the deformed shape after a corresponding FSI analysis. The results were computed using the Vertex Morphing method with a filter size of one fifth of the cylinder circumference.