Bayesian updating of engineering models with spatially variable properties
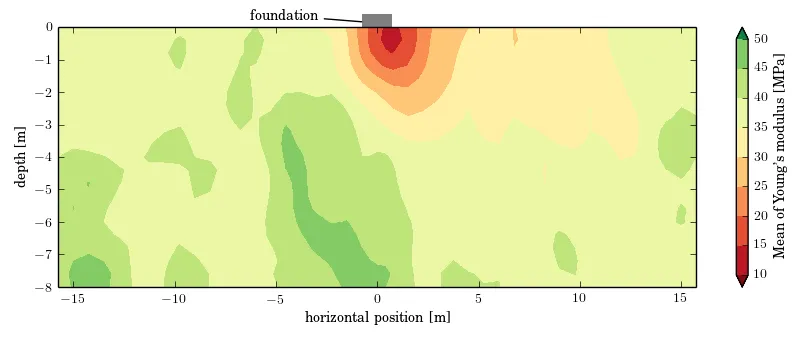
With advances in computation and monitoring technologies, there is a large number of possibilities for enhanced probabilistic predictions of engineering systems. It is becoming increasingly recognized that accurate predictions of such systems often require models that account for the random spatial variability of parameters. This holds in particular if monitoring and other observational data is to be used to learn the models and update predictions. In this project, the focus is on learning engineering models with spatially variable properties using Bayesian analysis. The Bayesian framework enables the combination of uncertain and incomplete information with sophisticated probabilistic models and it provides probabilistic information on the accuracy of the updated model. This project has two main goals: Firstly, we want to provide the first systematic investigation of the effect of different model choices on the posterior predictions, and provide recommendations for engineering practice. Secondly, we want to identify and further enhance efficient computational methods for Bayesian analysis of engineering models with discretized random fields.
Researchers
Selected publications
- Felipe Uribe, Iason Papaioannou, Youssef M. Marzouk, Daniel Straub. Cross-entropy-based importance sampling with failure-informed dimension reduction for rare event simulation. SIAM/ASA Journal on Uncertainty Quantification. 9(2), 818-847.
- Felipe Uribe, Iason Papaioannou, Jonas Latz, Wolfgang Betz, Elisabeth Ullmann, Daniel Straub. Bayesian inference with subset simulation in varying dimensions applied to the Karhunen–Loève expansion. International Journal for Numerical Methods in Engineering, 1-28.
- Jonas Latz (2020). On the well-posedness of Bayesian inverse problems, SIAM/ASA J. Uncertainty Quantification, 8 (1), 451-482.
- Felipe Uribe, Iason Papaioannou, Wolfgang Betz, Daniel Straub (2020). Bayesian inference of random fields represented with the Karhunen-Loève expansion, Computer Methods in Applied Mechanics and Engineering. 358, 112632.
- Christian Kahle, Kei Fong Lam, Jonas Latz, Elisabeth Ullmann (2019). Bayesian parameter identification in Cahn-Hilliard models for biological growth, SIAM/ASA J. Uncertainty Quantification, 7(2), 526–552.
- Jonas Latz, Marvin Eisenberger, Elisabeth Ullmann (2019). Fast sampling of parameterised Gaussian random fields, Computer Methods in Applied Mechanics and Engineering, 348, 978-1012.
- Jonas Latz, Iason Papaioannou, Elisabeth Ullmann (2018). Multilevel Sequential² Monte Carlo for Bayesian Inverse Problems, Journal of Computational Physics 368, p. 154-178
- Felipe Uribe, Iason Papaioannou, Wolfgang Betz, Elisabeth Ullmann, Daniel Straub (2017). Random fields in Bayesian inference: effects of the random field discretization. 12th International Conference on Structural Safety & Reliability (ICOSSAR 2017). Vienna, Austria.
- Felipe Uribe, Iason Papaioannou, Wolfgang Betz, Jonas Latz, Daniel Straub (2017). Bayesian model inference of random fields represented with the Karhunen-Loève expansion. International Conference on Uncertainty Quantification in Computational Sciences and Engineering (UNCECOMP 2017). Rhodes, Greece.
