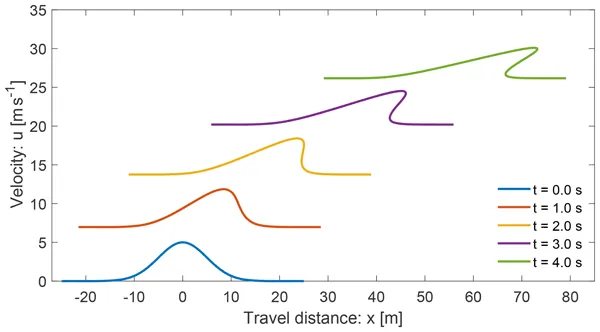
We present the first, simple and physics-based general analytical landslide velocity model that simultaneously incorporates the internal deformation (nonlinear advection) and externally applied forces, consisting of the net driving force and the viscous resistant. The model represents a novel class of nonlinear advective-dissipative system, where classical Voellmy and inviscid Burgers' equations are specifications of this general model. We show that the nonlinear advection and external forcing fundamentally regulate the state of motion and deformation, which substantially enhances our understanding of the velocity of a coherently deforming landslide. New solutions bridge the existing gap between negligibly deforming and massively deforming landslides through their internal deformations. This provides a novel, rapid, and consistent method for efficient coupling of different types of mass transports. The intrinsic mechanism of our solution describes the fascinating breaking wave and emergence of landslide folding. Landslide dynamics are architectured by advection and reigned by the system forcing. This provides practitioners with key information for instantly and accurately estimating the impact force that is very important in delineating hazard zones and for the mitigation of landslide hazards.
https://esurf.copernicus.org/articles/10/165/2022/esurf-10-165-2022.pdf