Multidisziplinäre Optimierung
Gegenstand der Multidisziplinären Optimierung (MDO) ist die Suche nach optimalen Lösungen für Systeme, die mit Hilfe von verschiedenen, interagierenden Simulationsdisziplinen analysiert werden. Typischerweise sind dies Systeme, die in natura gekoppelte Phänomene abbilden, wie z.B. die Fluid-Struktur-Wechselwirkung von Tragwerken im Strömungsfeld. Eine belastbare Optimierung stark gekoppelter Systeme setzt dabei voraus, dass diese Wechselwirkung berücksichtigt wird. MDO wird heute erfolgreich in verschiedenen Branchen eingesetzt. So z.B. in der Luft- und Raumfahrt, in der technische Disziplinen wie "Strukturmechanik", "Aerodynamik", "Regelungstechnik", aber auch wirtschaftliche Gesichtspunkte oft in enger Beziehung zueinander stehen.
Zur multidisziplinären Optimierung (insbesondere Formoptimierung) wird am Lehrstuhl eine modulare Simulationsumgebung entwickelt, mit der sowohl das notwendige Datenmanagement als auch die entsprechende Kopplungsalgorithmik realisiert werden kann. Alle Komponentnen sind dabei weitestgehend austauschbar eingesetzt. Komponenten die am Lehrstuhl diesbezüglich entwickelt werden sind: Primärlöser und adjungierte Verfahren, Werkzeuge zur Kontrolle der Netzqualität und Netzbewegung sowie gradienten-basierte Optimierungsverfahren.
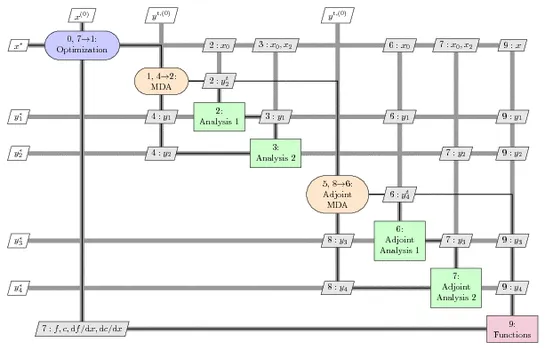
Ein implementiertes MDF-Verfahren ("Multi-Disciplinary Feasible") am Beispiel der Formoptimierung einer Struktur unter Windlast is oben schematisch dargestellt. Zur Simulation der Fluid-Struktur Wechselwirkung kommen verschiedene Kopplungsalgorithmen zum Einsatz. Zur effizenten Gradientenbestimmung werden desweiteren gekoppelte adjungierte Methoden angewandt.
Formoptimierung flexibler Strukturen innerhalb einer Strömung
Wie wichtig die Betrachtung einer gegebenen Kopplung im Optimierungsprozess sein kann, lässt sich schon an einfachen Beispielen nachvollziehen. So z.B. bei der Widerstandsoptimierung eines flexiblen Zylinders innerhalb eines laminaren Strömungsfeldes. Besonderer Fokus des Lehrstuhls liegt auf geometrisch nichtlinearen Strukturelementen. Demzufolge wurde der Zylinder mit nichtlinearen Schalenelementen modelliert.
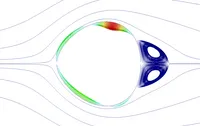
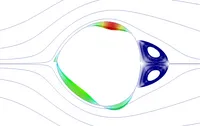
Die Gradientenanalyse durch gekoppelte adjungierte Methoden wurde entsprechend auf den Fall nichtlinearer Strukturen angepasst. Die zwei oberen Bilder rechts deuten die Unterschiede zwischen einer einfachen und einer multidisziplinären Optimierung an. Im obersten Bild sind Gradienten zu sehen, die aus einer ausschließlichen Betrachtung der Strömung stammen, wohingegen im mittleren Bild Gradienten aus einer gekoppelten adjungierten Gradientenanalyse gezeigt sind. Die unterschiedlichen Gradienten führen letztlich zu verschiedenen Lösungen.
Für den gekoppelten Fall ist ein Auszug der Formevolution im Bild rechts unten dargestellt. Eine Kombination der gekoppelten Gradientenanalyse mit knoten-basierter Formoptimierung, dem entsprechenden Filtering (Vertex Morphing) und der notwendigen Netzregularisierung liefert letztlich eine signifikante Optimierung ohne eine spezielle Parametrisierung des Zylinders einzuführen.